GMAT Book 1: Set Theory

Set Language Theory is a topic from which you could expect 1 to 3 questions in the GMAT quant section. Learn the topic by understanding the basics rather than just learning the formulae for union and intersection of sets. The topic is an important one.

Syllabus Covered in Wizako's GMAT Prep Book

Basic concepts of set theory such as union of sets, intersection of sets are tested in the GMAT in both variants - problem solving and data sufficiency. With a good grasp of the fundamental concepts governing set language, one should be able to attempt these questions with ease. Wizako's GMAT Math Lesson Book in this chapter covers the following concepts:

1. Introduction to the concept of sets and methods to represent sets.
2. Different types of sets explained with illustrative examples.
3. Cardinal number of sets, power sets, number of subsets for a set.
4. Definition of disjoint sets and null set.
5. The De-Morgan's Law.
6. Using Venn Diagrams to solve set language questions explained with illustrative examples.
7. Union and intersection of 2 sets
8. Union and intersection of 3 sets
9. Complement of a set
10. 9 solved examples, including Venn Diagram representation.
11. 5 Comprehensive exercise problems with answer key and explanatory answers.
12. A timed multiple choice test with 32 questions is provided as part of the work book. Detailed explanatory answers and answer key are provided for all questions in the test.

Here is a typical solved example in Wizako's GMAT Book | Set Theory

Sample Question

In a gathering of 50 people who have a red book or a white book, 30 have a red book and 16 have both a red book and a white book. How many among the 50 in the gathering have only a white book?

Explanatory Answer

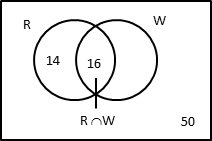
Number of people having a red book n(R) = 30
Number of people having a red and a white book n (R ∩ W) = 16

People in the gathering have a red book or a white book. i.e., everyone in the room has at least one of the two books.
This statement is very critical to determine the value of n (R ∪ W)
So, the total number of people in the room = number of people who have a red book or a white book = n (R ∪ W) = 50.

n (R ∪ W) = n(R) + n(W) - n(R ∩ W)
50 = 30 + n(W) - 16
50 - 14 = n(W) - 16
n(W) = 36
i.e., the number of people who have a white book = 36.

What is to be found?

Number of people who have only a white book.

Number of people who have only a white book = n(W) - n(R ∩ W) = 36 - 16 = 20

More in GMAT Set Theory